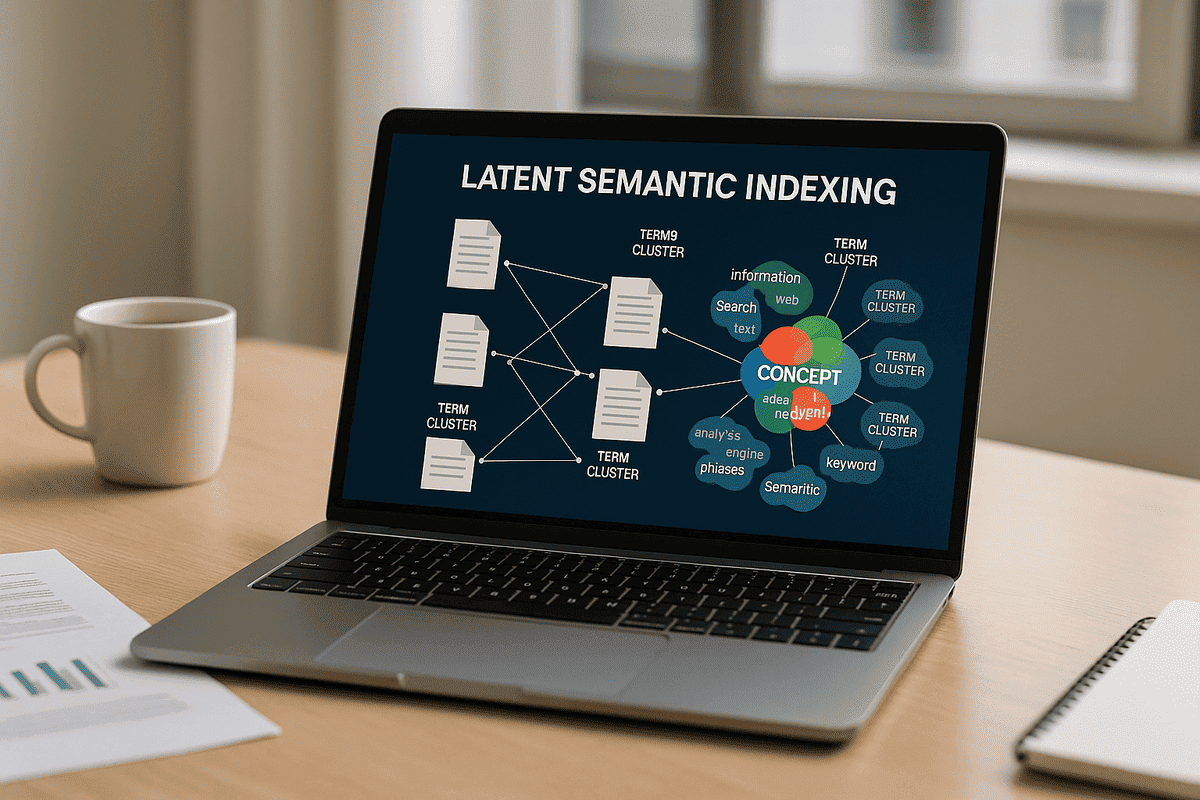
Latent Semantic Indexing (LSI) is a method used to find meaning in text. It checks how words appear together in different documents, not just the exact match. This helps find useful results even when the same words are not used.

LSI builds a term-document matrix and then applies Singular Value Decomposition (SVD) to reduce it. This step keeps the important patterns and removes noise.

It learns word groups from a similar context. For example, it links cars and automobiles because they appear in the same type of content. So, a search for “automobile” can also show documents about “cars.”

Some experts also call it Latent Semantic Analysis (LSA), but in text search and indexing, LSI is the common name.

Working Method of Latent Semantic Indexing

Latent Semantic Indexing (LSI) is a method used to understand the meaning of text by using maths to find patterns. It helps group documents and words that talk about similar things, even if they do not use the same exact words.

Step-by-step explanation:

1. Building a term-document matrix

• LSI starts by creating a large table called a term-document matrix.
• Rows = words (terms)
  Columns = documents
  Cells = how important a word is in that document
• To measure importance, it uses term frequency–inverse document frequency (TF-IDF).
• Most of this table is empty, because many words only appear in a few documents.

2. Applying Singular Value Decomposition (SVD)

• LSI uses Singular Value Decomposition (SVD) to break the matrix into 3 smaller parts:
  • U matrix → shows how words relate to hidden concepts
  • Σ matrix → holds numbers that show the strength of each concept
• V^T matrix → shows how documents relate to these concepts

3. Truncating the matrix

• LSI keeps only the top k singular values (usually 100–300)
• This step is called truncated SVD.
• It removes noise and keeps only strong patterns.
• This gives a smaller, easier-to-handle version of the original matrix.

4. Creating the latent semantic space

• After SVD, both words and documents are shown as vectors in a k-dimensional space.
• Words that appear in similar contexts move closer together.
• Documents that talk about similar topics also move near each other.

What this method helps with:

Concept-based retrieval

• LSI can match a search query to a document even if it does not contain the exact word.
• For example, if a user searches for “vehicle,” LSI may return documents about “cars,” because it understands the link between the two.

Handling vocabulary mismatch

• Synonymy: LSI groups words like car, automobile, and vehicle into one meaning.
• Polysemy: If a word has more than one meaning, LSI can use context to guess which one fits.

Better text search

• LSI does not need grammar rules or a dictionary.
• It works only by learning patterns from the statistical structure of text.
• This makes LSI language-neutral and usable in many languages without change.

Working with hidden topics

• LSI captures latent factors (hidden themes) in the data.
• Each factor is a mix of many words.
• These factors are not labeled, but users can look at top words in each to guess what the topic is.

Technical strength

• The low-rank approximation made by SVD keeps the most important part of the data.
• It gives the best possible result in terms of keeping information while reducing size.
• The top singular vectors carry the main patterns of word use across all documents.

How Latent Semantic Indexing Helps in Search

Improving keyword search with concept-based retrieval

Latent Semantic Indexing (LSI) was designed to fix common problems in keyword-based search. In most systems, different words may express the same idea (synonymy), or a single word may have more than one meaning (polysemy). These issues cause useful results to be missed or irrelevant ones to be shown.

LSI helps by learning latent concepts—hidden links between words used in similar contexts. It groups these words together in a shared space. This allows the system to return better results, even if the exact keyword is not present. This approach is called concept-based retrieval or semantic search.

For example, a search for “car” may return results containing “automobile” if both words are linked through how they appear in real documents. LSI uses co-occurrence patterns to match ideas, not just surface words.

Performance and recall in real systems

Tests on standard datasets like the TREC collections showed that reducing the model to about 300 latent dimensions gave better results than using all keywords. In about 20 percent of test cases, LSI gave a clear improvement. This worked by raising recall (finding more relevant documents) and in some cases even improving precision by removing unrelated noise.

Since LSI focuses on meaning, it works well in cross-language retrieval too. If trained on a multilingual dataset, it can link terms across languages without translation. This is possible because LSI depends only on the statistical structure of the text, not dictionaries or language tools.

Other uses and practical challenges

LSI has also been used for document clustering and text classification. Each document is stored as a vector of concept weights, so similar documents naturally stay close in the latent space. These concept values are then used in machine learning models to sort documents into topics.

Researchers also found that LSI’s automatic groupings often matched human judgments. It showed that the model could learn some of the same patterns people use to judge meaning.

But there are limits. Running Singular Value Decomposition (SVD) on large document sets takes a lot of memory and time. In early tests, LSI could only handle small datasets. Later, a method called folding-in was developed. It lets new documents be added without recomputing the whole model.

Even with this, LSI can still make errors. If a word has more than one meaning (polysemy), the system may mix them unless enough dimensions are kept. For example, the word “bank” could refer to a river or a money institution. Both may end up grouped unless the model has enough detail to tell them apart.

Still, LSI played a key role in the move from simple word match to semantic search. It helped pave the way for newer systems like probabilistic topic models, which also work by finding patterns in word use across large texts.

Use of Latent Semantic Indexing in Search Engines

Early use in small-scale search systems

Latent Semantic Indexing (LSI) was an early method to improve how search engines understood text. Instead of only matching exact words, it looked at the topic of both the search query and the document. Some early systems in the 1990s used LSI for enterprise search, where document sets were small and well managed.

These systems showed that concept-based indexing could return useful results even when the keywords did not match. For example, a query for airplane could bring up documents using the word aircraft, because LSI linked both through a latent semantic association. This helped with cases where different words meant the same thing.

But LSI did not scale well. Running Singular Value Decomposition (SVD) on billions of webpages with millions of terms was not possible with the computers of that time. So, large web search engines like Google chose other methods instead, like hyperlink analysis and probabilistic IR models.

Shift to modern semantic algorithms

As computers got faster, the search industry moved to newer and smarter tools. Google added semantic understanding to improve how it read queries and web pages—but not with LSI. Instead, it used machine learning and neural networks to learn what users really meant when they searched.

In 2015, Google introduced RankBrain, a machine learning algorithm that turned both queries and documents into vectors in a vector space. This made it easier to measure meaning, even if the words were different. Later, Google added BERT, a transformer-based model that could understand natural language better than any model before. These tools use embeddings—numeric codes that carry meaning—to find what the user is looking for.

These modern tools do something similar to what LSI aimed for, but they are more advanced, faster, and built using training data and deep learning, not manual matrix math.

SEO myths and the real role of LSI

Many in the SEO community still talk about LSI keywords, which they believe are related words that improve page ranking. In reality, Google has made it clear that LSI is not part of its search systems. Google’s John Mueller even said, “There is no such thing as LSI keywords.”

While LSI helped early tools understand word meaning, it is now considered outdated. One expert compared LSI to “training wheels” for search engines. Another said relying on LSI today is like trying to “connect to the mobile web using a smart telegraph.”

Still, LSI’s main idea—finding semantic links between terms—helped shape today’s search technology. But modern semantic search now runs on neural networks, large language models, and natural language processing, not LSI.
Use of Latent Semantic Indexing in Machine Learning and NLP

Latent Semantic Indexing (LSI) has been widely used beyond search systems. In machine learning and natural language processing (NLP), it works as a tool to turn text into simpler, useful data. LSI helps by reducing high-dimensional text into a smaller semantic space, which keeps meaning but removes noise.

Text as vectors for classification

LSI is often used in feature engineering. It converts text into concept vectors that carry the most important meanings. Instead of using thousands of raw word counts, LSI creates compact vectors that can be used in models like support vector machines (SVM) or neural networks. This makes it easier for the model to find patterns. It has been useful in tasks like document classification, where news articles, emails, or customer service messages are sorted by topic.

One example is spam filtering. Spammers often hide words to avoid detection, but LSI focuses on meaning, not just words. Emails are mapped into a latent concept space, and spam messages tend to form their own clusters. With this, LSI helps spot spam even when exact keywords are missing.

Topic discovery and clustering

Before newer models came, LSI was one of the first ways to do topic modeling. When looking at the top words in each SVD dimension, one could often guess a latent topic. For example, a concept that loads heavily on doctor, hospital, and patient would likely represent a medical topic.

In document clustering, LSI is also helpful. It places each document in a vector space where related documents stay closer. Tools like k-means clustering use this space to group documents better than raw keyword-based methods.

LSI has also been used in information visualization. Because it reduces data to a smaller space, one can plot documents on 2D or 3D graphs. Related topics show up as nearby points, making it easier to spot themes in the text.

Use in education and language research

The same math used in LSI is also called Latent Semantic Analysis (LSA). In cognitive science and educational tools, it has helped model how people learn words and understand meaning. LSA can compare a student’s essay with a set of reference texts and judge how well it matches the topic. This is done without labels—just by measuring semantic similarity.

Current role and legacy

In modern NLP, LSI is no longer the top method. Today, tools like Word2Vec, BERT, and other neural network-based models create better vector embeddings. These models understand context, work across large text sets, and perform better in most tasks.

Still, LSI is fast, simple, and useful when working with smaller data or when clear interpretation is needed. It does not need training data, and it runs quickly on moderate text sizes. In some projects, LSI remains a practical choice for unsupervised tasks or where computing power is limited.

Even though LSI is not used in modern large-scale models, it helped introduce the idea of text as geometry—turning meaning into a shape in space. This concept led to many of the tools used in NLP today.

Comparison of Latent Semantic Indexing with TF‑IDF

Term Frequency–Inverse Document Frequency (TF‑IDF) is a method that gives weight to words based on how often they appear in a document and how rare they are across all documents. This makes important words stand out while reducing the value of very common words like “the” or “and”. Most keyword-based search systems use TF‑IDF to rank documents using vectors, where each word is treated as a separate feature.

Latent Semantic Indexing (LSI) builds on this same idea. It uses a term-document matrix, and the values in this matrix are usually weighted with TF‑IDF before running LSI. This helps avoid letting common words dominate the process.

The key difference is how the two systems treat word meaning:

• TF‑IDF keeps every word as its own feature. It creates large, sparse vectors, with one dimension for each unique word.
• LSI, on the other hand, reduces these vectors by finding hidden patterns. It uses Singular Value Decomposition (SVD) to combine words that often appear together into a latent feature or semantic factor.

For example, if “airplane” and “aircraft” appear in similar documents, TF‑IDF sees them as unrelated, but LSI can group them together in the same latent concept.

How LSI goes beyond TF‑IDF

TF‑IDF is useful for improving basic search by giving better word scores. But it does not see relationships between words. If two documents use different words for the same topic, TF‑IDF may not link them.

LSI solves this by reducing the size of the data and discovering semantic structure. The vectors produced by LSI reflect the meaning behind the text, not just the surface terms. It helps address the term mismatch problem, where people use different words to describe the same idea.

It is important to note that LSI does not replace TF‑IDF—it uses it. TF‑IDF makes the input cleaner, and LSI adds meaning by finding deeper patterns. Together, they form a strong method:

• TF‑IDF finds important words.
• LSI finds how those words relate.

In modern systems, newer models like topic models and neural embeddings handle both tasks at once. But LSI was one of the first to show that reducing dimensions and focusing on meaning can improve how we search and organize text.

Relation of Latent Semantic Indexing (LSI) to Singular Value Decomposition (SVD)

Singular Value Decomposition (SVD) is the core mathematical method behind Latent Semantic Indexing (LSI). The main idea of LSI is to apply truncated SVD to a term-document matrix to reduce the number of dimensions while keeping the most important patterns in word usage. This creates what are known as latent semantic factors.

SVD takes any matrix and breaks it into three parts: two orthogonal matrices that show word and document relationships, and a diagonal matrix of singular values that reflect the strength of each concept. In LSI, the original matrix is large and sparse, usually filled with TF‑IDF weighted term counts. SVD is then used to keep only the top k singular values, removing weaker signals from the data. This step helps reduce noise and highlight stronger word associations, much like smoothing or dimensionality reduction.

Why SVD is used in LSI

SVD has an important benefit: for any fixed number of dimensions, the truncated SVD gives the best possible approximation of the original matrix. This means that LSI can keep as much useful information as possible while using fewer features. This is why SVD is considered an optimal linear method for learning structure from text.

In LSI, we do not subtract the mean like we do in Principal Component Analysis (PCA), because that step does not work well for text data. But both PCA and SVD use eigen-decomposition, and the effect is similar—reducing large data into a simpler space that still holds meaning.

Each latent dimension in LSI explains a unique pattern in word usage. These dimensions are orthogonal, meaning they do not overlap, and each one adds something new to how the system understands the text. This structure makes LSI stable and deterministic. Unlike some machine learning models, it does not depend on random guesses or multiple runs.

Limitations and impact

SVD also has limits. It does not know anything about language rules or topic boundaries. It only works based on co-occurrence patterns in the data. So the semantic factors it finds may mix different themes, and the results can be hard to explain. Also, SVD is not designed for live systems. If you add new documents, you often need to recompute the full decomposition or use an approximate method like folding-in.

Still, the idea of using SVD for text was a breakthrough in the late 1980s. LSI showed that linear algebra could solve real problems in information retrieval by finding deep patterns hidden in how words are used. This helped move the field away from manual rules and simple keyword matching.

Comparison of Latent Semantic Indexing (LSI) with Latent Dirichlet Allocation (LDA)

Latent Dirichlet Allocation (LDA) and Latent Semantic Indexing (LSI) are both methods used for finding hidden topics in text. While they aim for the same goal—reducing large collections of text to latent semantic themes—their approaches are very different.

Generative model versus linear algebra

LDA is a probabilistic generative model. It treats each document as a mix of topics, and each topic as a group of words with assigned probabilities. In this system:

• A document is built by picking a set of topics.
• Each word is then selected from one of those topics, based on the topic’s word distribution.

This creates a model that learns which words belong to which topics, and how much each topic contributes to each document. The output is a topic mixture per document and a set of word probabilities per topic. These outputs are easy to read and label. For example, a topic with high weights on doctor, hospital, and patient can be clearly identified as related to medicine.

LSI does not follow this structure. It uses Singular Value Decomposition (SVD) to reduce a term-document matrix into latent dimensions. There is no built-in model of how documents are created. LSI simply compresses data to uncover patterns in how terms appear together. The result is a semantic space, but it lacks the probabilistic structure found in LDA.

Handling meaning and interpretation

LDA can manage polysemy more naturally. Since a word can appear in more than one topic, LDA lets the meaning change with context. LSI assigns one vector to each word, which may mix different senses. Also, LDA gives each topic a clear interpretation based on word probabilities, while LSI’s factors are mathematical combinations that are harder to explain.

Another difference is in how new documents are handled. LDA can directly assign topic probabilities to new text. LSI cannot do this without using a workaround called folding-in, which only approximates the position of the new document in the existing space.

Performance and practical use

Studies have shown that LDA often performs better than LSI on tasks like predicting unseen documents or modeling word distributions. It can achieve lower perplexity, a measure of how well the model fits new data. For example, research by Blei and others showed that LDA outperformed both unigram models and probabilistic LSI (pLSI) on benchmark datasets.

However, LDA is more complex. Training LDA requires steps like Gibbs sampling or variational inference, which are slower than a single SVD used in LSI. Because of this, LSI is sometimes preferred for faster or smaller-scale tasks. It can be useful when simple semantic grouping is enough and exact modeling is not required.

In modern use, many systems rely on LDA or newer tools like neural topic models. But LSI is still relevant in teaching, small-scale projects, or cases where interpretability and speed matter.

Shared influence and legacy

LSI and LDA have influenced each other over time. The probabilistic LSI (pLSI) model came between the two, adding some probability ideas to LSI. LDA then built on that to form a complete generative model. Even today, some matrix factorization and hybrid topic models use SVD from LSI for fast starting points.

While LDA is more advanced in theory, both models helped shape how modern systems understand language. Each shows a different way of finding meaning in text—LSI with linear algebra, and LDA with probability.